4.4.4 Integration using partial fraction decomposition
Partial fraction decomposition is used to prepare a rational function
for integration. A rational function is the quotient of two
polynomials:

To integrate a rational function, four major steps are performed.
- Reduce the rational; this is only performed when the dividend is a polynomial of higher degree than that of the divisor .
- Decompose the denominator into irreducible linear and quadratic factors.
- Find a partial-fraction decomposition of the factors. (See §3.4.9.)
- Finally, integrate the decomposition.
The steps for an example are summarized in Figure 4.1. Column b contains expressions resulting from transformations on expressions in column a.
| Step | a. | b. | |
| 1 | 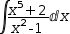 |
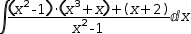 |
|
| 1.1 | 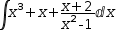 |
||
| 2 | 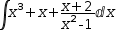 |
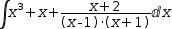 |
|
| 3 | 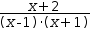 |
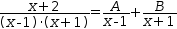 |
|
| 3.1 |  |
||
| 3.2 |  |
||
| 3.3 |  |
||
| 3.4 | 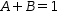 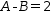 |
||
| 3.5 | 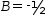 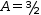 |
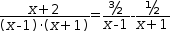 |
|
| 4 |  |
 |
The summary above is considerably condensed. Here are the missing details.
1.b Perform Polynomial Division on the integrand to reduce the rational.
1.1b Distribute the fraction, Simplify , collect terms with the same denominator and Simplify again.
2.b Reduce
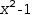
3.b Select the rational function as a subexpression of the integral and apply Partial Fraction .
3.1.b In the equation introduced by 3.b, rearrange the denominator on the left to be a multiplicand on the right.
3.2.b Distribute the new multiplicand across the former right side.
3.3.b Distribute the expression on the right. Collect terms in x and factor.
3.4.a Use selection and partial duplication,
 , along with + to create the equations
, along with + to create the equations
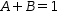
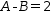
3.5.b Substitute A and B into 3.b
4.a Select the rational function in 2.b and substitute from the right side of 3.5.b.
4.b Transform the integral using symbolic simplification.